$3.1.11.$ Две пружины жесткости $k$, соединенные, как показано на рисунке, не деформированы. Какой массы груз следует подвесить к точке соединения пружин, чтобы он опустился на малое расстояние $x$ в положение равновесия?
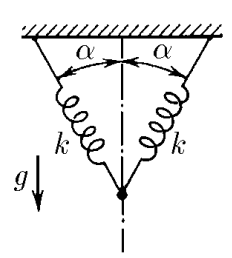
Каждая пружина будет иметь силу упругости при растяжении $$F_y=k\Delta l=kx\cos\alpha$$ Условие равенства сил $$mg=2F_y\cos\alpha =2kx\cos^2 \alpha$$ Откуда, масса груза $$\boxed{m=\frac{2kx\cos^2 \alpha}{g}}$$
$$m=\frac{2kx\cos^2 \alpha}{g}$$