$3.1.5.$ Длина нити математического маятника $l$, масса шарика $m$. Определите силу, действующую на шарик, при отклонениях его от положения равновесия на $x$ в случае, если $x\ll l$. Как зависит от $x$ потенциальная энергия шарика?
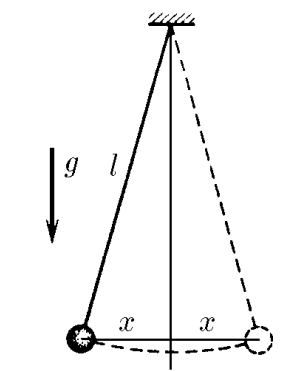
При отколонении маятника на него действует возвращающая сила $F$ действующая в направлении противоположной направлению скорости, которая является возвращающей и равной $$OX:F=-mg\sin\varphi=\fbox{$-mg\frac{x}{l}$}$$ Учитывая, что колебания явлеются гармоническими, то их амплитуда не большая, а величина отклонения много меньше длины нити: $(x\ll l)$. Воспользуемся выражением для малых углов $\cos\alpha\approx1-\frac{\alpha^2}{2};\quad\sin\alpha\approx\alpha$ $$1-\cos\alpha\approx\frac{x^2}{2l^2}$$ Изменение положения шарика по-вертикали $$\Delta h = l \cdot (1-\cos\alpha )=\frac{x^2}{2l}$$ Откуда изменение потенциальной энергии $$\Delta U = mg\cdot\Delta h = \boxed{mg\frac{x^2}{2l}}$$
Альтернативно, можно было бы рассписать изменение энергии как интеграл совершенной работы на промежутке $dx$: $$U=\int_{0}^{U}dU=\int_{0}^{x}mg\frac{x}{l}dx=\boxed{\frac{mgx^2}{2l}}$$
$$F=-mg\frac{x}{l};\quad U=\frac{mgx^2}{2l}$$