$3.1.7.$ Горизонтальный желоб слева от нижней линии выгнут по цилиндрической поверхности радиуса $r$, а справа — по поверхности радиуса $R$. Определите отношение наибольших отклонений влево и вправо при малых колебаниях тела в этом желобе.
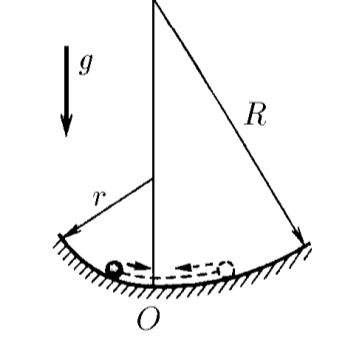
По закону сохранения энергия тела максимальная потенциальная энергия будет сохраняться в обеих случаях $$E_{p1}=E_{p2}$$ А следовательно и высота $h$ поднимется относительно нижней точки траектории на которую поднимется тело будут равны
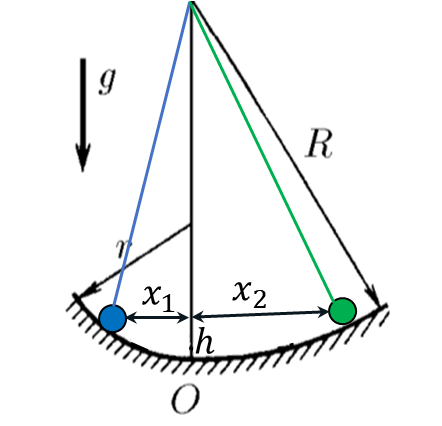
Воспользуемся выражением $\Delta U$ для малых колебаний полученное в 3.1.5 $$\Delta U = \frac{mgx_1^2}{2r}=\frac{mgx_2^2}{2R}$$ Откуда следует, что $$\boxed{\frac{x_2}{x_1}=\sqrt{\frac{R}{r}}}$$
$$\frac{x_2}{x_1}=\sqrt{\frac{R}{r}}$$