$3.1.9.$ Шарик массы $m$ и радиуса $r$ скользит по поверхности лунки, радиус кривизны которой $R$. Найдите зависимость потенциальной энергии шарика от малого смещения $x$ из положения равновесия.
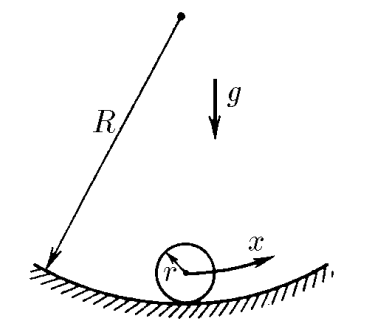
Также как и в 3.1.5, предложим два варианта решения: через малые преращения и через интегрирование
При отклонении тела по горизонтали на малую величину $x$, его высота изменяется на величину $$h=R'-\sqrt{{R'}^2-x^2}=R'\left(1-\sqrt{1-\frac{x^2}{{R'}^2}}\right)\quad(1)$$ Где $R'$ — расстояние от центра кривизны до центра масс шарика $$R'=R-r$$ Учитывая, малость $x$ $$x\ll R'\Leftrightarrow \frac{x}{R'}\ll 1$$ Так мы можем воспользоваться approximation $(1+\xi )^a\approx 1+\xi a$, где $\xi\ll 1$ $$\left(1-\frac{x^2}{{R'}^2}\right)^{1/2}=1-\frac{x^2}{2{R'}^2}$$ Подставляем в $(1)$ $$h=R'\cdot \frac{x^2}{2{R'}^2}=\frac{x^2}{2R'}$$ Подставляем в формулу для потенциальной энергии $$U=mgh=mg\frac{x^2}{2R'}$$ Подставляя значение для $R'$, получаем финальное выражение $$\boxed{U=\frac{mgx^2}{2(R-r)}}$$
Именение энергии при малом изменении координаты можно найти по определению $$dU=Fdx$$ При этом горизонатльная сила, которая будет возвращать шарик в устойчивое равновесие найдём с учётом малости угла $\varphi$ $$F=mg\sin\varphi=mg\frac{x}{R-r}$$ Откуда потенциальную энергию найдём через интегрирование $dU$ $$U=\int_{0}^{U}dU=\int_{0}^{x}mg\frac{x}{R-r}dx=\frac{mg}{R-r}\int_{0}^{x}xdx$$ Данный интеграл решается как $$\int_{0}^{x}xdx=\frac{mg}{R-r}\cdot\frac{x^2}{2}$$ Откуда потенциальная энергия шарика $$\boxed{U=\frac{mgx^2}{2(R-r)}}$$
$$U=\frac{mgx^2}{2(R-r)}$$