Условие:

$3.2.11.$ Найдите частоту малых колебаний системы, описанной в задаче 3.1.10.

Решение:

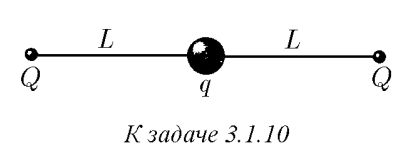
Второй закон Ньютона $$m\ddot{x}(t)-F=0$$ Где суммарную внешнюю силу найдём из закона Кулона $$F=kqQ\left(\frac{1}{(L-x)^2}-\frac{1}{(L+x)^2}\right)$$ Используясь приближением для малого значения $$x =\frac{h}{R} \ll 1; \quad(1+x)^\alpha\approx 1+\alpha x$$ $$F=-\frac{4kqQLx}{(L^2-x^2)^2}\approx-\frac{4kqQx}{L^3}$$ Уравнение гармонических колебаний $$\ddot{x}(t)+\frac{4kqQx}{mL^3}x(t)$$ Получаем искомую частоту малых колебаний $$\boxed{\omega =\sqrt{\frac{4kqQ}{mL^3}}=\sqrt{\frac{qQ}{m\pi\varepsilon_0L^3}}}$$

Альтернативное решение:

Ответ: $\omega =\sqrt{\frac{qQ}{m\pi\varepsilon_0L^3}}$.