$3.2.12.$ Определите время полета камня от одного полюса Земли до другого по прямому тоннелю, прорытому через центр. Плотность Земли считать постоянной, ее радиус — равным 6400 км.
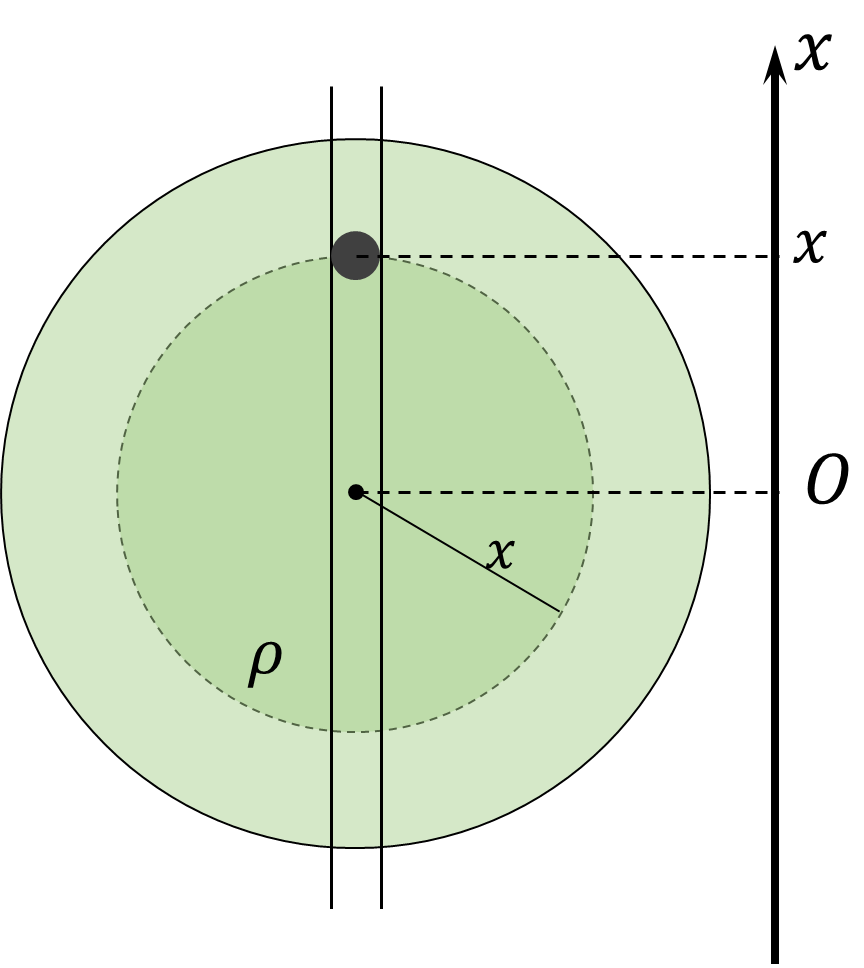
На тело, на расстоянии $x$ от ядра, будет действовать гравитационная сила притяжения вызванная внутренними слоями планеты плотности $\rho$, образующих шар радиуса $x$. Масса этой части земли $$M_\oplus = \frac{4}{3} \rho\pi x^3$$ Гравитационная сила, дествующая на камень на глубине $x$ $$F_G = \frac{GmM_\oplus}{x^2}=mg\frac{x}{R}$$ Второй закон Ньютона $$m\ddot{x}(t)=-\frac{mg}{R}x(t)$$ Запишем уравнение гармонических колебаний $$\ddot{x}(t)+\frac{g}{R}x(t)=0$$ Угловая частота таких колебаний $$\omega =\sqrt{\frac{g}{R}}\Rightarrow T=2\pi\sqrt{\frac{R}{g}}$$ Т.к. нас интересует время полёта только в одну сторону, поэтому берём половину этого периода $$\boxed{t=\frac{T}{2}=\pi\sqrt{\frac{R}{g}}=42\text{ min}}$$
$$t=42\text{ min}$$