$3.2.13.$ В Земле прорыт прямой тоннель, не проходящий через ее центр. Определите время движения поезда с выключенными двигателями по такому тоннелю, если влиянием вращения Земли на движение поезда и трением пренебречь.
Аналогично 3.2.12, внешнюю силу $F$ найдём как
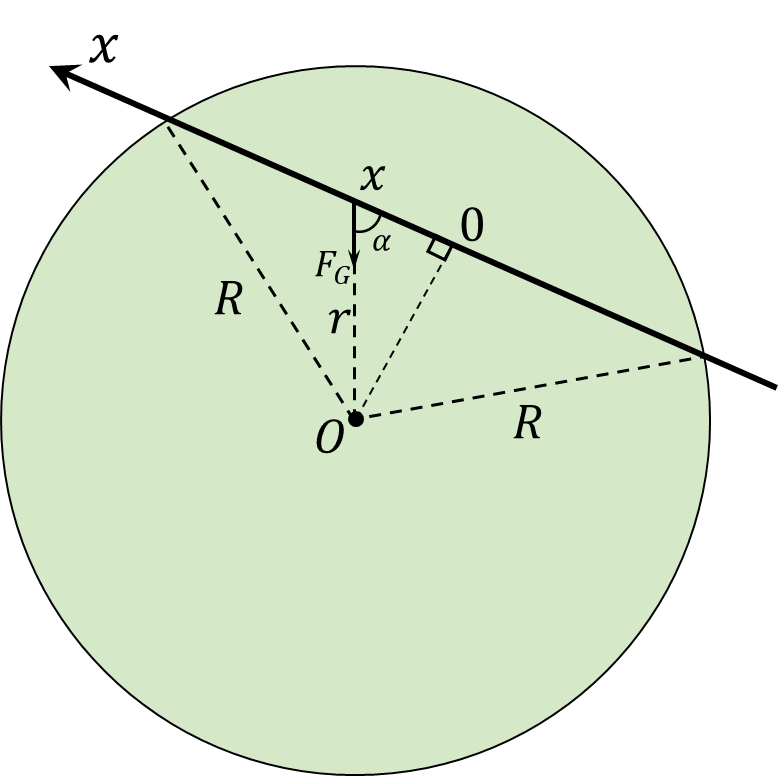
На тело, на расстоянии $x$ от ядра, будет действовать гравитационная сила притяжения вызванная внутренними слоями планеты плотности $\rho$, образующих шар радиуса $x$. Масса этой части земли $$M_\oplus = \frac{4}{3} \rho\pi x^3$$ Гравитационная сила, дествующая на камень на глубине $x$ $$F_G = \frac{GmM_\oplus}{x^2}=mg\frac{x}{R}$$ При этом только горизонтальная компонента этой силы будет создавать момент. Откуда, результирующая внешняя сила равна $$F=mg\cos\alpha =mg\frac{x}{R}$$ Отсюда находим угловую частоту колебаний $$\omega =\sqrt{\frac{g}{R}}$$ Период колебаний в данной системе $$T=2\pi\sqrt{\frac{R}{g}}$$ Т.к. нас интересует время полёта только в одну сторону, поэтому берём половину этого периода $$\boxed{t=\frac{T}{2}=\pi\sqrt{\frac{R}{g}}\approx42\text{ min}}$$
$$t=42\text{ min}$$