Условие:

$3.2.18.$ Шарик массы $m$, насаженный на стержень, вращается с угловой скоростью $\Omega$ вокруг оси O, с которой он соединен пружиной жесткости k. Определите частоту колебаний шарика вдоль пружины, если $\Omega^2 < k/m$.

Решение:

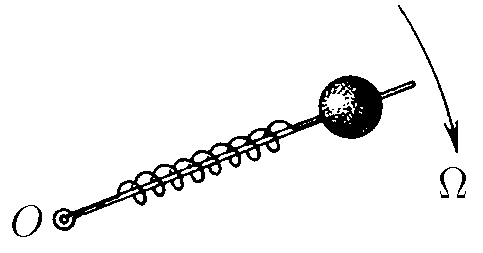
$m\ddot{x}(t)+kx-m\Omega^2x=0$

$\ddot{x}(t)+(\frac{k}{m}-\Omega^2)x(t)=0$

$\omega =\sqrt{\frac{k}{m}-\Omega^2}$

Альтернативное решение:

Ответ: $\omega =\sqrt{\frac{k}{m}-\Omega^2}$.