Условие:

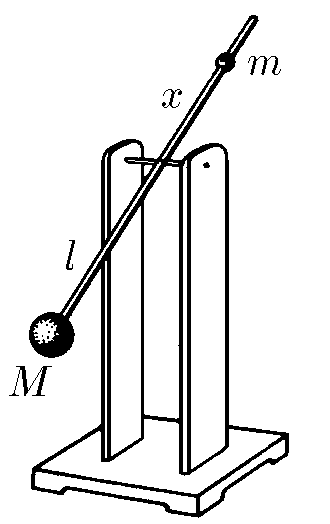
$3.2.19.$ Метроном представляет собой легкий стержень, на нижнем конце которого на расстоянии $l$ от оси находится груз массы $M$. Выше оси подвижный грузик массы $m$ можно закреплять на стержне на разных расстояниях $x$ от оси, тем самым подбирая нужную частоту колебаний метронома. Считая массы точечными, найдите, как частота колебаний зависит от расстояния $x$.

Решение:

$I\varepsilon =\sum_{}^{}M=mgx\sin\varphi-Mgl\sin\varphi$$\approx\varphi(mgx-Mgl)$

$I=Ml^2+mx^2$

$(Ml^2+mx^2)\ddot{\varphi}+\varphi(Mgl-mgx)=0$

$\ddot{\varphi}+\frac{Mgl-mgx}{Ml^2+mx^2}\varphi=0$

$\omega =\sqrt{\frac{g(Ml-mx)}{Ml^2+mx^2}}$

Альтернативное решение:

Ответ: $\omega =\sqrt{\frac{g(Ml-mx)}{Ml^2+mx^2}}$.