$3.2.20.$ Как изменится частота колебаний маятника, представляющего собой груз на легком стержне, если к середине стержня прикрепить горизонтальную пружину жесткости $k$? На рисунке изображено состояние равновесия.
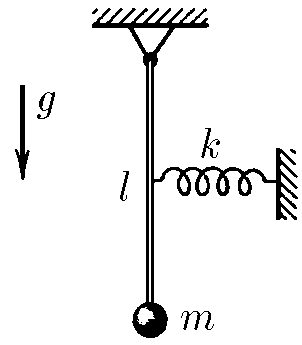
$\omega =\sqrt{\frac{\alpha}{\beta}}$
$E_k=\frac{m\upsilon^2}{2}\Rightarrow \beta =\frac{m}{2}$
$E_p=mgl(1-\cos\varphi)+\frac{k(x/2)^2}{2}$$=\frac{mgl\varphi^2}{2}+\frac{kx^2}{8}$$=\frac{mgl}{2}\frac{x^2}{l^2}+\frac{kx^2}{8}$$=x^2(\frac{mg}{2l}+\frac{k}{8})$$\Rightarrow \alpha$$=\frac{mg}{2l}+\frac{k}{8}$
$\omega^2=\frac{g}{l}+\frac{k}{4m}$
