Условие:

$3.2.21.$ К ободу колеса с горизонтально расположенной осью прикрепили грузик массы $m$. Найдите массу колеса, предполагая ее однородно распределенной по ободу, если частота колебаний колеса с грузиком вокруг оси равна $\omega$, а его радиус равен $R$, $R< g/\omega^2$ .

Решение:

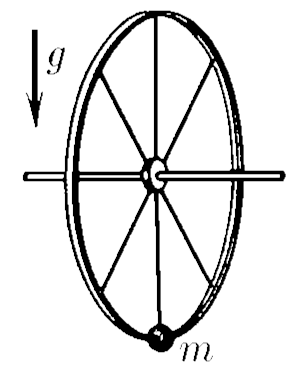
$I\varepsilon =\sum_{}^{}M$

$I=MR^2+mR^2=R^2(M+m)$

$R^2(M+m)\ddot{\varphi}+mgR\sin\varphi=0$

$\ddot{\varphi}+\frac{mg}{R(M+m)}\varphi=0$

$\omega^2=\frac{mg}{R(M+m)}\Rightarrow M=m(\frac{g}{\omega^2R}-1)$

Альтернативное решение:

Ответ: $M=m(\frac{g}{\omega^2R}-1)$.