Условие:

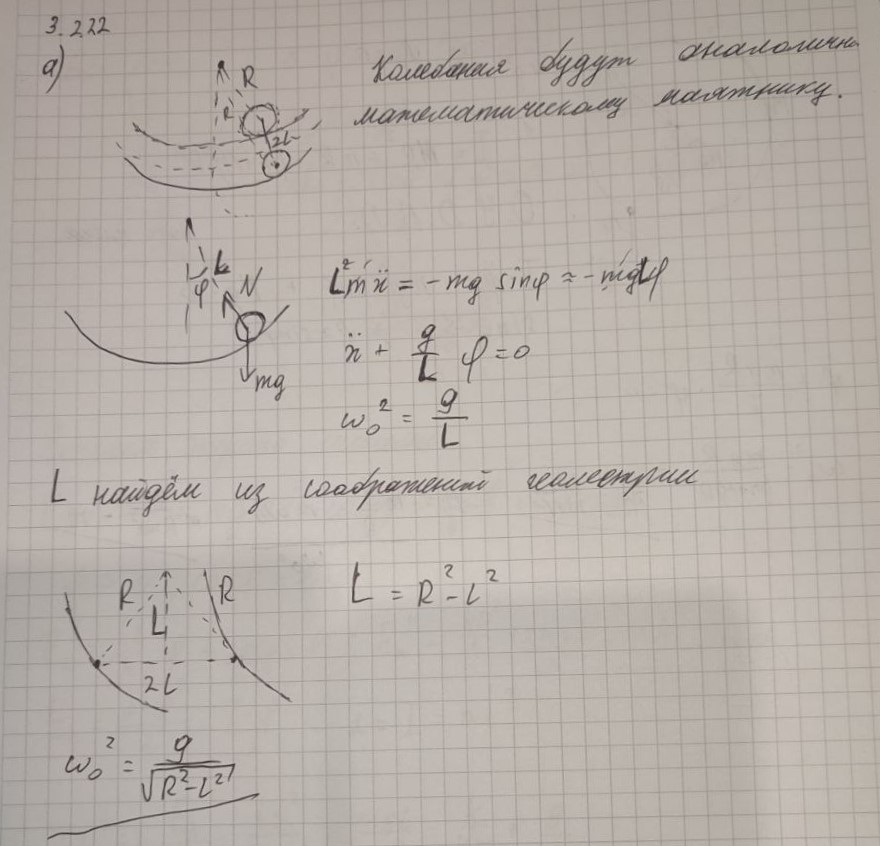
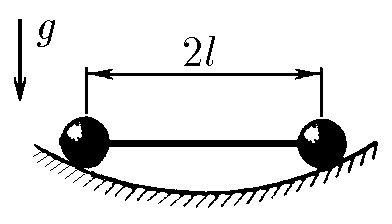
$3.2.22.$ В сферической лунке радиуса $R$ находятся две точечные массы, соединенные невесомым стержнем длины $2l$. Определите частоту колебаний при движении в направлении: а) перпендикулярном плоскости рисунка; $б^ ∗$ ) параллельном этой плоскости.

Решение:

а) $2m\ddot{x}(t)+2mg\sin\varphi=0$

$\ddot{x}(t)+\frac{g}{\sqrt{R^2-l^2}}x(t)=0$

$\omega^2=\fbox{$\frac{g}{\sqrt{R^2-l^2}}$}$

б) $\omega^2=\frac{\alpha}{\beta}$

$E_p=2mgR'(1-\cos\varphi)$$=2mg\sqrt{R^2-l^2}(1-\cos\varphi)$$\approx \frac{2mg\sqrt{R^2-l^2}}{2}\varphi^2$

$\alpha =\frac{2mg\sqrt{R^2-l^2}}{2}$

$E_k=\frac{2m\upsilon^2}{2}=\frac{2m\omega^2R^2}{2}=\frac{2mR^2}{2}\dot{\varphi}^2$

$\beta =\frac{2mR^2}{2}$

$\omega^2=\fbox{$\frac{g\sqrt{R^2-l^2}}{R^2}$}$

Альтернативное решение:

Ответ: $\omega^2=\frac{g}{\sqrt{R^2-l^2}}$, $\omega^2=\frac{g\sqrt{R^2-l^2}}{R^2}$.