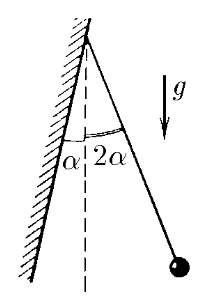
$3.3.11.$ К наклонной стене подвешен маятник длины $l$. Маятник отклонили от вертикали на малый угол, в два раза превышающий угол наклона стены к вертикали, и отпустили. Найдите период колебаний маятника, если удары о стену абсолютно упругие.
Ниже представлена анимация движения маятника, описанного в условии задачи
Перед просмотр решения рекомендую посмотреть решение аналогичной задачи 3.3.5
Угол поворота нити математического маятника описывается как $$\varphi(t) = \varphi_0 \cos\omega t$$ В данном случае максимальный угол отклонения составляет $$\varphi_0 = 2\alpha$$ Время за которое тело могло бы поднимяться от угла $\alpha$ до $2\alpha$ описывается уравнением $$\cos\omega t = \frac{1}{2}$$ $$\omega t = \frac{\pi}{3}$$ $$t = \frac{\pi}{3}\sqrt{\frac{l}{g}}$$ За это же время маятник мог бы опуститься от $2\alpha$ до $\alpha$
Но т.к. тело упраго ударяеться о стенку, то переход $\alpha\rightarrow 2\alpha\rightarrow \alpha$ происходит мгновенно
Тогда полное время в пути(период одного колебания) уменьшается на $2t$ $$T = 2\pi\sqrt{\frac{l}{g}}-2\frac{\pi}{3}\sqrt{\frac{l}{g}}$$ $$\boxed{T = \frac{4\pi}{3}\sqrt{\frac{l}{g}}}$$
$$T = \frac{4\pi}{3}\sqrt{\frac{l}{g}}$$