$3.3.5.$ Найдите период колебаний математического маятника длины $l$, если на пути нити на расстоянии $l/2$ вниз по вертикали от точки подвеса вбит гвоздь.
Ниже представлена анимация движения маятника, описанного в условии задачи
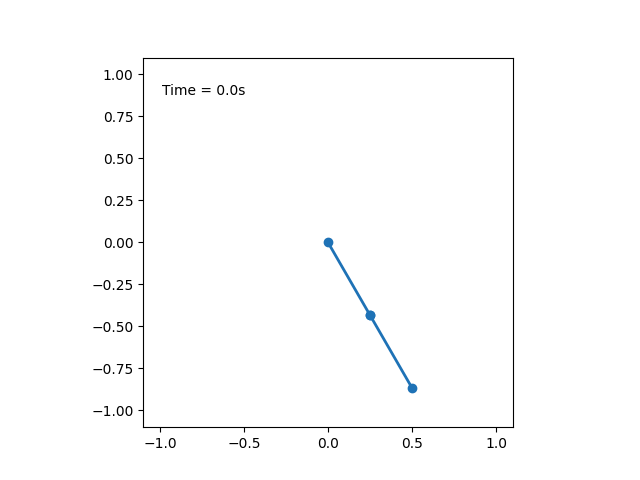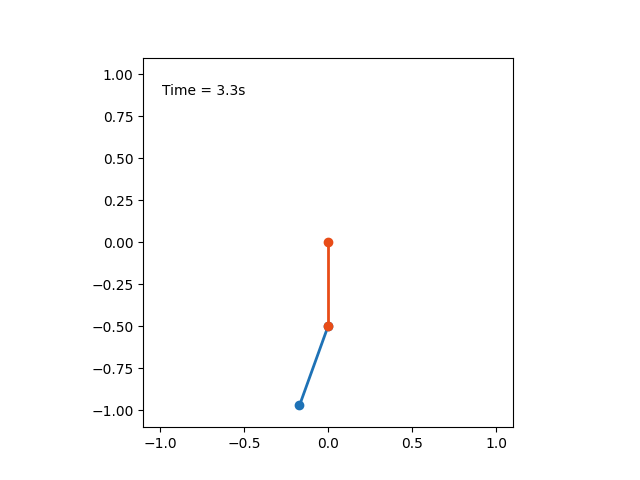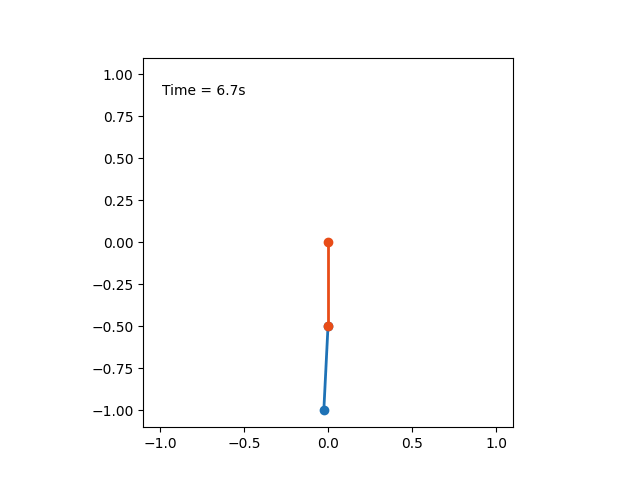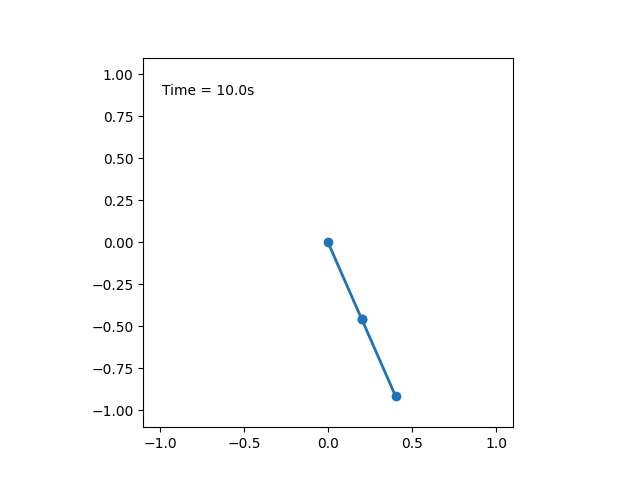
Первую часть пути "до гвоздя", маятник пройдет за время $$T_1 = \frac{1}{2} 2 \pi\sqrt{\frac{l}{g}} = \pi\sqrt{\frac{l}{g}} \quad \text{(1)}$$ После соударения с гвоздем, половина его длина остается на месте, а остальная половина продолжает движение с той же скоростью
Таким образом, длина маятника уменьшается вдвое $$l\rightarrow \frac{l}{2}$$ Делая замену в $\text{(1)}$ $$T_2 = \pi\sqrt{\frac{l}{2g}}$$ Таким образом полный период колебаний $$T = T_1+T_2$$ $$\boxed{T = (1 + 1/ \sqrt{2} )\pi\sqrt {\frac{l}{g}}}$$
$$T = (1 + 1/ \sqrt{2} )\pi\sqrt {\frac{l}{g}}$$