$3.3.6.$ Найдите период колебаний тела в задаче 3.1.7
$3.1.7.$ Горизонтальный желоб слева от нижней линии выгнут по цилиндрической поверхности радиуса $r$, а справа — по поверхности радиуса $R$. Определите отношение наибольших отклонений влево и вправо при малых колебаниях тела в этом желобе.
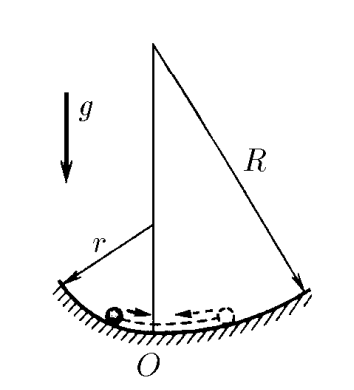
Аналогично 3.3.5, колебания будут состоять из двух половинных-колебаний
Когда тело скользит по желобу радиуса $R$, его движение, с точки зрения кинематики, ни чем не отличается от движения математического маятника с длинной нити $R$
Таким образом, период колебаний составляет $$T_0 = 2\pi\sqrt{\frac{R}{g}}$$ Т.е. половину желоба, он пройдет за время $$T_1 = \pi\sqrt{\frac{R}{g}}$$ Аналогично, для желоба радиуса $r$ $$T_2 = \pi\sqrt{\frac{r}{g}}$$ Таким образом полный период колебаний $$T = T_1+T_2$$ $$\boxed{T = \pi (\sqrt{\frac{R}{g}}+\sqrt{\frac{r}{g}})}$$
$$T = \pi (\sqrt{\frac{R}{g}}+\sqrt{\frac{r}{g}})$$