$5.6.22^*.$ В откачанном пространстве вертикально стоит цилиндрический сосуд, перекрытый сверху подвижным поршнем массы $M$. Под поршнем находится одноатомный газ при температуре $T$ и давлении $P$. Внутреннее сечение цилиндра $S$, высота той части сосуда, внутри которой находится газ, $H$. Поршень отпустили. Он начал двигаться. Чему равна максимальная скорость, развиваемая поршнем, если газ сжимается изотермически? адиабатически?
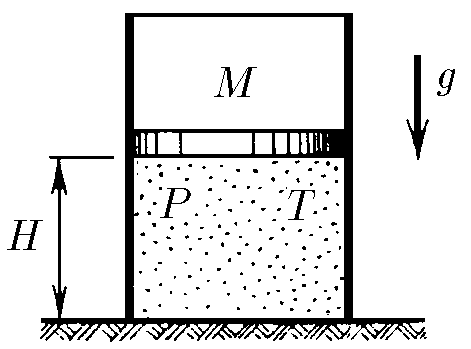
a) Из закона сохранения энергии или теоремы о кинетической энергии и работе $$\frac{Mv^2}{2} = Mg(H-y) + A \quad(1)$$ где $A$ - работа, совершенная над поршнем, равная работе, совершенной газом, которая в данном случае (изотермический процесс) определяется как $$A = nRT\ln{\frac{Sy}{SH}} = -nRT\ln{\frac{H}{y}} \quad(2)$$ Подставляя $(2)$ в $(1)$ $$\frac{Mv^2}{2} = Mg(H-y) - nRT\ln{\frac{H}{y}} \quad(3)$$ Из закона Бойля-Мариотта $$PSH = P'Sy \quad(4)$$ Применение уравнения состояния к начальному состоянию, $$n = \frac{PSH}{RT} \quad(5)$$ $$PSH = nRT$$ Применение второго закона Ньютона $$Mg - P(t)S = M\frac{dv}{dt}$$ В момент максимальной скорости $dv/dt = 0$ и $P(t) = P'$, следовательно $$Mg = P'S \quad(6)$$ Подставляя $(6)$ в $(4)$ и выражая $y$ $$y = \frac{PSH}{Mg} \quad(7)$$ Подставляя $(5)$ и $(7)$ в $(3)$ и выделяя $v$ $$\boxed{v = \sqrt{2gH\left(1-\frac{PS}{Mg}+\frac{PS}{Mg}\ln{\frac{PS}{Mg}}\right)}}$$ b) Из закона Пуассона $$P(SH)^\gamma = P'(Sy)^\gamma\quad(8)$$ Работа, совершаемая газом при адиабатическом процессе, равна $$A = \frac{PSH-P'Sy}{\gamma -1} \quad(9)$$ Согласно $(6)$, мы можем модифицировать $(8)$ и выразить $y$, получив $$y = H\left(\frac{PS}{Mg}\right)^\frac{1}{\gamma} \quad(10)$$ Подставляем $(9)$ в $(1)$ и учитываем $(6)$,
$$\frac{Mv^2}{2} = H\left(Mg+\frac{PS}{\gamma -1}\right)-Mgy\left(1+\frac{1}{\gamma -1}\right) \quad(11)$$
Подставляя $(10)$ в $(11)$, поскольку газ одноатомный ($i = 3$ и $\gamma = 5/3$), и отделяя $v$ $$\boxed{v = \sqrt{2gH\left[1-\frac{5}{2}\left(\frac{PS}{Mg}\right)^\frac{3}{5}+\frac{3}{2}\frac{PS}{Mg}\right]}}$$