6.1.17. Чему равна напряженность электрического поля в центре равномерно заряженного тонкого кольца радиуса $R$? Чему она равна на оси кольца на расстоянии $h$ от центра? Заряд кольца $Q$.
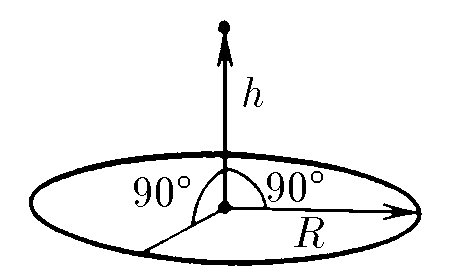
В центре кольца два одинаковых противоположных небольших участка кольца создают напряжённости, равные по модулю и противоположные по направлению. По принципу суперпозиции результирующая напряжённость есть векторная сумма всех элементарных напряжённостей $\vec{E}=\sum\vec{E_i}$. Сумма противоположных по направлению векторов равна $vec{0}$, а значит результирующая напряжённость равна нулю. На расстоянии h от центра кольца проекции элементарных напряжённостей на плоскость кольца аналогичным образом скомпенсируются, но их проекции на ось кольца останутся. $(E_i)_{Oh}=E_i \cdot \sin{\alpha}$, где $\alpha$ - угол наклона $\vec{E_i}$ к плоскости кольца ($\tan{\alpha}=h/R$). $E=\sum{(E_i)_{Oh}}=\sum{E_i \cdot \sin{\alpha}}$$=\sum{\frac{1}{4\pi\varepsilon_0}\frac{\Delta{Q}}{R^2+h^2}\cdot \frac{h}{\sqrt{R^2+h^2}}}$, где $\Delta{Q}$ - заряд малого участка, $\sum{\Delta{Q}}=Q$ $E=\frac{1}{4\pi\varepsilon_0}\frac{Qh}{(R^2+h^2)^{3/2}}$