$6.1.7.$ Три заряда $q_1$, $q_2$, $q_3$ связаны друг с другом двумя нитями. Длина каждой нити $l$. Найдите их силу натяжения.
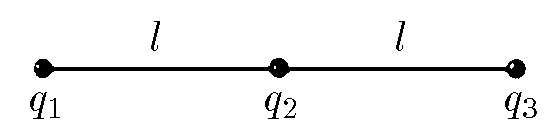
В установившемся режиме заряды будут покоиться, т.е. действие всех сил на них будет скомпенсированно. Запишем второй закон Ньютона для каждого из зарядов: $$ \left\{ \begin{gathered} F_{12}+F_{13}-T_{12}=0\quad(1) \\ F_{12}+T_{12}-F_{23}-T_{23}=0\quad(2) \\ F_{23}+F_{13}-T_{23}=0\quad(3) \\ \end{gathered} \right. $$ Расспишем силу Кулона, взаимодействия зарядов $$ \left\{ \begin{gathered} \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{\ell^2}+\frac{1}{4\pi\varepsilon_0}\frac{q_1q_3}{(2\ell)^2}-T_{12}=0\quad(4) \\ \frac{1}{4\pi\varepsilon_0}\frac{q_1q_2}{\ell^2}-\frac{1}{4\pi\varepsilon_0}\frac{q_2q_3}{\ell^2}+T_{12}-T_{23}=0\quad(5) \\ \frac{1}{4\pi\varepsilon_0}\frac{q_2q_3}{\ell^2}+\frac{1}{4\pi\varepsilon_0}\frac{q_1q_3}{(2\ell)^2}-T_{23}=0\quad(6) \\ \end{gathered} \right. $$ Из уравнений $(1),(3)$ найдём силу натяжения нитей $T_{12}$ и $T_{23}$
$$\boxed{T_{12}=\frac{1}{4\pi\varepsilon_0}\frac{q_1(4q_2+q_3)}{4\ell^2};\quad T_{23}=\frac{1}{4\pi\varepsilon_0}\frac{q_3(4q_2+q_1)}{4\ell^2}}$$
$$\frac{q_1(4q_2+q_3)}{16\pi\varepsilon_0\ell^2}\parallel \frac{q_3(4q_2+q_1)}{16\pi\varepsilon_0\ell^2}$$