$6.6.20^{∗}.$ С какой силой втягивается диэлектрическая пластина в плоский конденсатор с зарядом $Q$, когда она входит в пространство между обкладками на длину $x$? Диэлектрическая проницаемость пластины $\varepsilon $, а толщина ее немного меньше расстояния между обкладками $d$. Размеры обкладок, как и пластины, $a × b$.
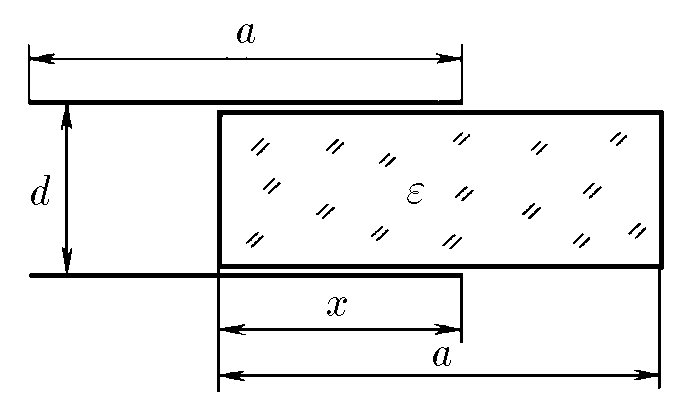
Емкость конденсатора представит емкость паралельных конденсаторов $C_1$ и $C_2$ для обкладок размера $a × b$ $C_1 = \frac{\varepsilon_0 b}{d}(a-x)$ $C_2 = \frac{\varepsilon_0 b x\varepsilon }{d}$ $C = C_1+C_2=\frac{\varepsilon_0 b[a+x(\varepsilon -1)]}{d}$ Расчитаем энергию $E=\frac{Q^2}{2C}$ этого конденсатора: $E_С=\frac{Q^2d}{2\varepsilon_0 b[a+x(\varepsilon -1)]}$ Находим $F$ силу через приращение энергии $dE$: $dE=F\cdot dx$ $F=\frac{dE}{dx}$ $F=-\frac{Q^2d(\varepsilon -1)}{2\varepsilon_0 b[a+x(\varepsilon -1)]^2}$ При этом "$-$" при $F$ показывает, что сила, является втягивающейся