$6.6.21.$ В широкий сосуд с жидкостью ставится вертикально плоский конденсатор так, что нижняя часть пластин конденсатора погружается в жидкость. Конденсатор подключён к батарее, которая поддерживает на обкладках конденсатора разность потенциалов $V$. Расстояние между пластинами конденсатора $d$, плотность жидкости $\rho$, диэлектрическая проницаемость $\varepsilon $. Жидкость несжимаема. На какую высоту поднимется жидкость? Поверхностным натяжением пренебречь.
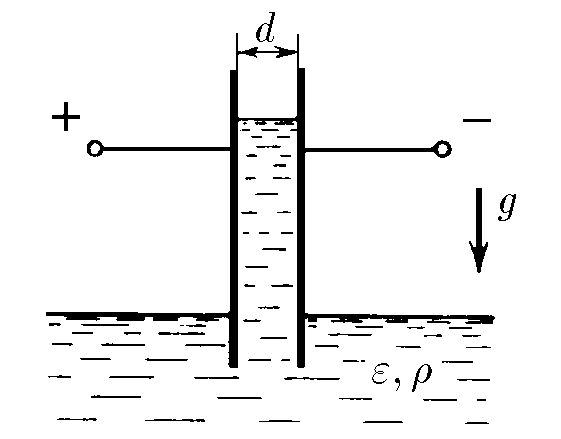
Пусть столб жидкости поднялся на высоту $h$ Емкость конденсатора представит емкость паралельных конденсаторов $C_1$ и $C_2$
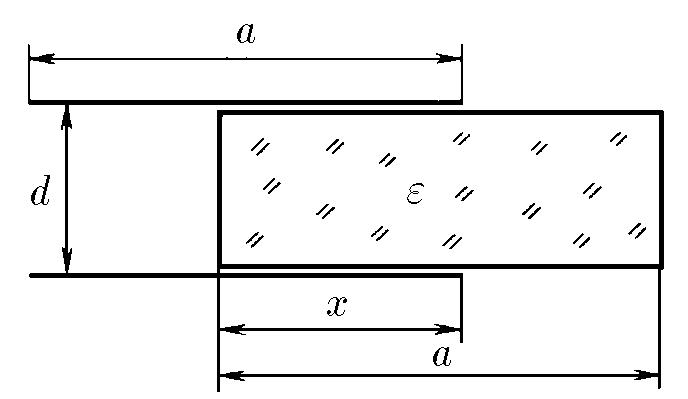
Что является предыдущещей 6.6.20 Емкость конденсатора представит емкость паралельных конденсаторов $C_1$ и $C_2$ для обкладок размера $a × a$ $C_1 = \frac{\varepsilon_0 a}{d}(a-x)$ $C_2 = \frac{\varepsilon_0 a x\varepsilon }{d}$ $C = C_1+C_2=\frac{\varepsilon_0 a}{d}(a+x(\varepsilon -1))$ Расчитаем энергию $E=\frac{CV^2}{2}$ этого конденсатора: $E_С=\frac{\varepsilon_0 a V^2}{2d}(a+x(\varepsilon -1))$ Потенциальная энергия столба жидкости составит: $E_P=-\rho g da \frac{h^2}{2}$ Полная энергия: $E=E_P+E_С=-\rho g da \frac{h^2}{2}+\frac{\varepsilon_0 a V^2}{2d}(a+h(\varepsilon -1))$ Будет минимальна при $\frac{dE}{dh}=0$: $\frac{\varepsilon_0(\varepsilon -1) a V^2}{2d}-\rho g dah=0$ $h=\frac{\varepsilon_0 (\varepsilon -1)V^2}{2 \rho gd^2 }$