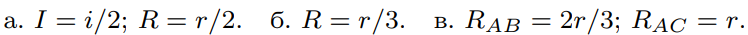$8.3.27^*.$ а. Если в бесконечной схеме, состоящей из квадратных ячеек, через один узел $A$ подводят ток $i$, а через соседний узел $B$ отводят ток $i$, то какой ток идет по сопротивлению, соединяющему узлы $A$ и $B$? Каково эквивалентное сопротивление цепи между этими узлами, если сопротивление стороны ячейки $r$? б. Каково эквивалентное сопротивление между соседними узлами бесконечной кубической арматуры, если сопротивление ребра куба $r$? в. Определите сопротивление между узлами $A$ и $B$ двумерной бесконечной сетки с ячейками в виде правильных шестиугольников и узлами $C$ и $A$, расположенными через один соседний узел. Сторона каждой ячейки имеет сопротивление $r$.
а) Предположим, что напряжение между точками $A$ и $B$ равно $V$, тогда $V=IR=I_0R_0,$ где $R$ - сопротивление всей сетки, $I$, ток через сетку и $I_0$, ток через сегмент $AB$. Тогда из симметрии $I/4$ является частью тока, протекающего по всем четырем проволочным сегментам, встречающимся в точке А, и аналогично количество тока, протекающего по проводам, встречающееся в $В$, равно $I/4$. Таким образом, ток $I/2$ проходит через проводник $AB$, т.е. $I_0=I_2$ Следовательно, $R=\frac{R_0}{2}$