$8.4.7.$ Какой заряд протечет через гальванометр после замыкания ключа? Какое количество теплоты выделится на сопротивлении?
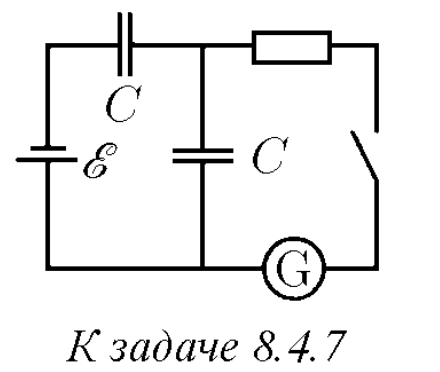
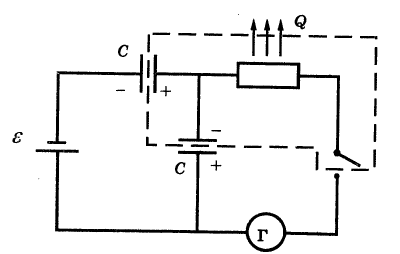
До замыкания ключа простой расчет дает: $\varepsilon = \frac{q_{1}}{C} + \frac{q_{1}}{C} = \frac{2q_{1}}{C}, \quad(1)$ где $q_1$ — заряд каждого из конденсаторов. После замыкания ключа с установлением равновесного распределения зарядов (прекращения тока в цепи) нижний конденсатор не заряжен, а заряд верхнего определяется из уравнения: $\varepsilon = \frac{q_{2}}{C} \quad(2)$ Чтобы определить заряд, прошедший через гальванометр, мысленно выделим часть схемы, обозначенную пунктиром. До замыкания ключа суммарный заряд этой части схемы равен нулю, после замыкания — заряду положительной обкладки верхнего конденсатора $q_2$. Таким образом, через гальзаиометр прошел заряд $q_{2} = \varepsilonC$. Для вычисления выделившейся на сопротивлении теплоты воспользуемся законом сохранения энергии. До замыкания ключа энергия двух конденсаторов: $W_{1} = 2 \cdot \frac{q_{1}^{2}}{2C} = \frac{ \varepsilon^{2}C}{4}$. После замыкания ключа энергия схемы за исключением батареи равна: $W_{2} = \frac{q_{2}^{2}}{2C} + Q = \frac{C \varepsilon ^{2}}{2} +Q, \quad(4)$ где $Q$ — количество теплоты, выделившейся на сопротивлении. Согласно закону сохранения энергии, изменение энергии $W_{2} - W_{1}$ равно работе сторонних сил батарей: $W_{2} - W_{1} = A_{ст} = \varepsilon \Delta q \quad(5)$ с учетом равенства нулю величины внутреннего сопротивления батареи. Величина заряда $\Delta q$, прошедшего через батарею, равно изменению заряда на левой обкладке верхнего конденсатора: $q_{2} - q_{1} = \Delta q = C \varepsilon - \frac{1}{2} C \varepsilon = \frac{1}{2} C \varepsilon \quad(6)$ Подставляя $(3)$, $(4)$ и $(6)$ в $(5)$, находим: $Q = \frac{C \varepsilon ^{2}}{4}$