$8.4.8.$ Диод имеет вольт-амперную характеристику, изображенную на рисунке. При напряжении $V_0$ диод открывается. Конденсатор вначале не заряжен. Какое количество теплоты выделится на сопротивлении после замыкания ключа?
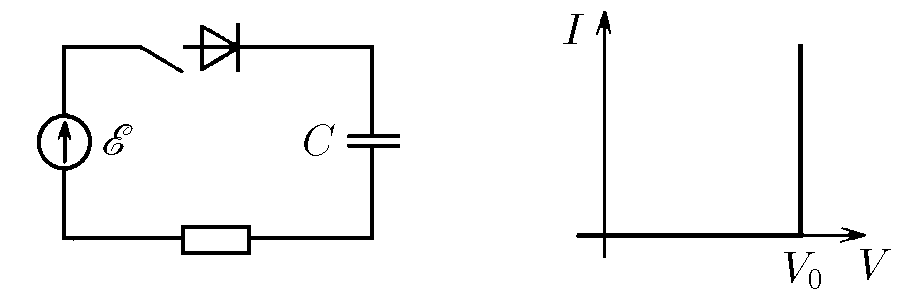
Рассмотрим случай, когда ЭДС батареи $\varepsilon > U_{0}$. Пусть сразу после замыка ния ключа ток в цепи равен $I_0$. Закон Ома для замкнутой цепи в этом случае будет иметь вид $\varepsilon = U_{0} + I_{0}R$, откуда $I_{0} = \frac{ \varepsilon - U_{0}}{R}$. Появившийся ток в цепи начнет заряжать конденсатор но по мере зарядки ток будет уменьшаться, и при напряжении на конденсаторе, равном $\varepsilon - U_{0}$, ток в цепи прекратится. Это будет новое стационарное состояние: ток $I=0$, а заряд на конденсаторе $$q = C( \varepsilon - U_{0} )$$ За время зарядки конденсатора батарея совершит работу $$A = C( \varepsilon - U_{0}) \varepsilon$$ Часть этой работы пойдет на работу по преодолению разности потенциалов $U_0$ внутреннею электрического поля диода: $$A_{д} = qU_{0} = C( \varepsilon - U_{0})U_{0}$$ Вторая часть работы перейдет в энергию, запасенную конденсатором: $$W_{к} = \frac{q^{2} }{2C} = \frac{C( \varepsilon - U_{0} )^{2} }{2}$$ И наконец, оставшаяся часть работы выделится в виде тепла в резисторе: $$Q = A - A_{д} - W_{к} $$ $$Q = C( \varepsilon - U_{0} ) \varepsilon - C( \varepsilon - U_{0} )U_{0} - \frac{C ( \varepsilon - U_{0})^{2} }{2}$$ После перегрупировки $$Q = C( \varepsilon - U_{0} ) \left ( \varepsilon - U_{0} - \frac{ \varepsilon - U_{0} }{2} \right ) = \frac{C ( \varepsilon - U_{0} )^{2} }{2}$$
$$W=C({E}-V_0)^2/2, \varepsilon>V_0;\quad W=0, \varepsilon < V_0$$