$9.1.12.$ Виток радиуса $R$ согнули по диаметру под прямым углом и поместили в однородное магнитное поле индукции B так, что одна из плоскостей витка оказалась расположенной под углом $\alpha$, другая — под углом $\frac{\pi}{2}-\alpha$ к направлению индукции $B$. Ток в витке $I$. Определите момент сил, действующих на виток.
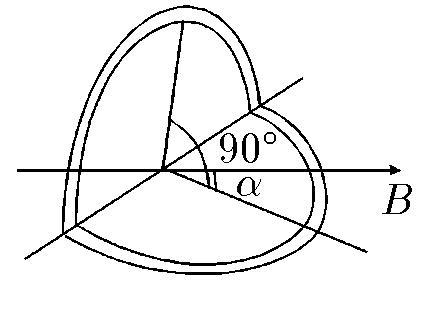
Разобьем контур на два контура с одинаковым током, но в разных плоскостях.
Найдем момент сил для каждого из них: $$M_1 = \frac{1}{2}\pi R^2IB\cdot \sin\alpha$$ $$M_2 = \frac{1}{2}\pi R^2IB\cdot \sin\left(\frac{\pi}{2} -\alpha\right) = \frac{1}{2}\pi R^2IB\cdot \cos\alpha$$ Суммарный момент сил $$\boxed{M = M_1 + M_2 = \frac{1}{2}\pi R^2IB\cdot (\sin\alpha + \cos\alpha )}$$
$$M = \frac{1}{2}\pi R^2IB\cdot (\sin\alpha + \cos\alpha )$$