$9.1.14.$ Кольцо радиуса $R$, по которому циркулирует ток $I$, поместили в неоднородное аксиально-симметричное поле. Ось кольца совпадает с осью симметрии магнитного поля. Индукция магнитного поля $B$, действующего на ток, направлена под углом $\alpha$ к оси симметрии поля. Масса кольца $m$. Определите ускорение кольца.
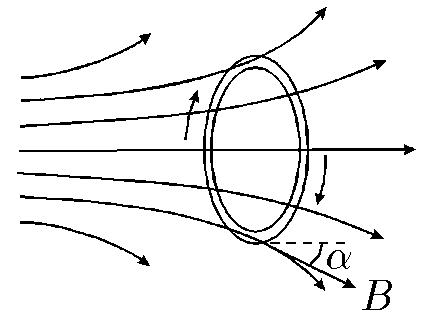
Ускорять кольцо будет тангенциальная составляющая магнитной индукции $B_{|}$ так как её перпендикулярная составляющая $B_\bot$ направленна на деформацию кольца.
В каждой точке кольца это $B\sin\alpha$ так как ускорение не меняет направление при повороте $dl$ то: $$ma = 2\pi RIB\sin\alpha\Rightarrow \boxed{a = 2\pi\frac{RIB\sin\alpha}{m}}$$
$$a = 2\pi\frac{RIB\sin\alpha}{m} $$