$9.1.3.$ На линейный проводник длины $l$, расположенный перпендикулярно магнитному полю, действует сила $F$, если ток в проводнике равен $I$. С какой силой магнитное поле будет действовать на:
а) изогнутый под углом $\varphi$ проводник длины $l + L$, если плоскость изгиба перпендикулярна магнитному полю, а ток в проводнике равен $I_1$
б) проводник в виде полуокружности радиуса $R$, по которому течет ток $I_2$, если плоскость полуокружности перпендикулярна магнитному полю?
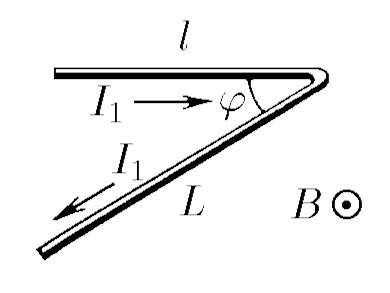
а) Из закона Ампера, находим индукцию магнитного поля $B$ $$F_1 = Il \cdot B \Rightarrow B = \frac{F}{Il}\quad(1)$$ при этом, чилы действующие на части провода с токами $I_1$ и $I_2$, соответсвенно $$F_1 = I_1l \cdot B; \quad F_2 = I_1L\cdot B$$ Подставляем $(1)$: $$F_1= \frac{I_1}{I}F; \quad F_2 = \frac{I_1L}{Il}F$$ Силу, действующую на изогнутый под углом $\varphi$ кусок провода, найдём из теоремы косинусов $$|\vec{F_p}| = |\vec{F_1} + \vec{F_2}| = \sqrt{{F_1}^2+{F_2}^2+2 F_1 F_2\cdot\cos\varphi}$$ $$\boxed{|\vec{F_p}| = F\frac{I_1}{I}\sqrt{1+\frac{L^2}{l^2} + 2\frac{L}{l}\cdot\cos\varphi}}$$ б) Для проводника из полуокружности, поспользуемся всё той же формулой для индукции магнитного поля $B$ $$B = \frac{F}{Il}$$ На малую часть проводника длиной $dl$, действует сила Ампера $$dF = B I_2~dl = B I_2R~d\theta$$ Для нахождения силы $F$ проинтегрируем силы, действующие на каждую часть полукольца $$F = \int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos\theta dF = BI_2R\int\limits_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos\theta~d\theta$$ После математических преобразований, получаем силу действующую на полукольцо $$\boxed{F = 2BI_2R = 2F\frac{I_2R}{Il}}$$
$$F\frac{I_1}{I}\sqrt{1+\frac{L^2}{l^2} + 2\cos\varphi\frac{L}{l}};\quad2F\frac{I_2R}{Il}$$