$9.1.6.$ Квадратная рамка с током закреплена так, что может свободно вращаться вокруг горизонтально расположенной стороны. Рамка находится в вертикальном однородном магнитном поле индукции $B$. Угол наклона рамки к горизонту $\alpha$, ее масса $m$, длина стороны $a$. Найдите ток в рамке.
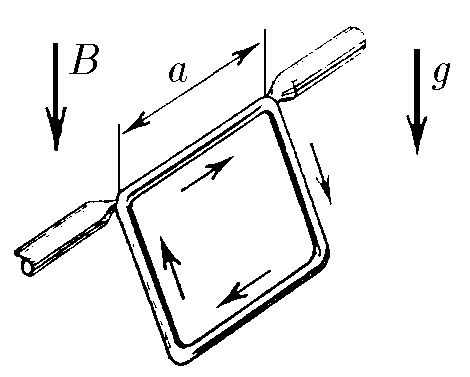
Момент сил действующих на рамку со стороны магнитного поля вызванный силой Ампера $$M_B = Fa = Ba^2I\sin\alpha$$ Момент силы тяжести: $$M_{mg} = mg\cdot \frac{a}{2}\cos\alpha$$ В условии равновесия, сумма моментов внешних сил, с учётом направления, равна нулю $(M_B = M_{mg})$: $$ B \sin\alpha~\cdot aI = \frac{1}{2}mg\cdot \cos\alpha$$ Откуда находим ток в рамке $$\boxed{I = \frac{mg\cdot \cot\alpha}{2Ba}}$$
$$I = \frac{mg\cdot \cot\alpha}{2Ba} $$