$9.1.7.$ В однородном магнитном поле поместили прямоугольную рамку с током. Индукция магнитного поля B параллельна плоскости рамки. Площадь рамки $S$, ток в ней $I$.
а) Докажите, что момент сил, действующий на рамку, $N = BM$, где $M = IS$ — магнитный момент рамки.
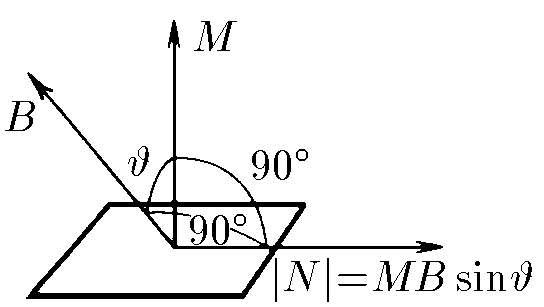
б) Докажите, что момент сил, действующий на рамку в случае, когда индукция магнитного поля направлена так, как изображено на рисунке, равен $\vec{N} =[\vec{M} \times \vec{B} ]$ где $M$ — магнитный момент рамки, модуль которого равен $IS$, а направление перпендикулярно плоскости рамки.
а) Момент сил будут создавать линии рамки перпендикулярные линиям магнитной индукции $B$. Пусть рамка имеет размеры $a$ на $b$ (для определённости, будем считать $b \bot B$), тогда момент силы Ампера будет составлять: $$N = 2\cdot |\vec{Ib} \times \vec{B}|\cdot \frac{a}{2} = Ib \cdot B \cdot a$$ учитывая площадь рамки $(S = ab)$, то момент сил, действующий на рамку $$\boxed{\boxed{N = IBS = BM}}$$
б) перпендикулярная компонента магнитной индукции $B_{\bot}$ будет направленно на растяжение рамки и не будет создавать момент силы $(N=0)$, между тем момент создаваемый $B_{|}$ составляет $$N = B_{|}IS = BIS\sin\alpha =|\vec{IS} \times \vec{B}|$$ так как $\vec{N} = \vec{F} \times \vec{r}$, то будет справедливо, что $\vec{N} = \vec{IS} \times \vec{B}$, потому что направление момента перпендикулярно силе и плечу силы $$\boxed{\boxed{\vec{N} = \vec{M} \times \vec{B}}}$$