$9.2.1.$ Электрическое поле напряженности $E~$ зарядов, движущихся со скоростью $v$, создает магнитное поле, индукция которого $\vec{B} = K[\vec{v}\times \vec{E}]$. Коэффициент $K$ равен $\varepsilon_0 \mu_0$ в СИ и $1/c$ в СГС, где $c$ — скорость света. Докажите, что магнитное взаимодействие двух движущихся зарядов слабее их электрического взаимодействия.
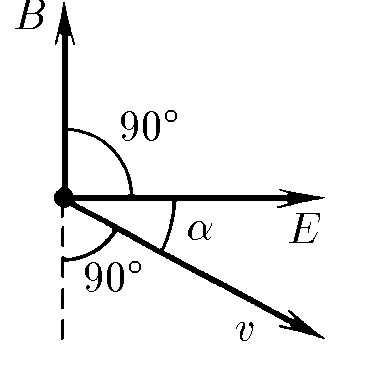
Магнитное поле, индукция которого $$|\vec{B}| = \varepsilon_0 \mu_0\left[\vec{v}\times \vec{E}\right] \le \varepsilon_0 \mu_0vE$$ тогда сила магнитного взаимодействия (сила Лоренца) зарядов $$F_B = |q[\vec{v} \times \vec{B}]| = qvB \le \varepsilon_0 \mu_0 qv^2E$$ учитывая, силу электростатического взаимодействия $F_E = qE$, получаем $$\frac{F_B}{F_E} \le \varepsilon_0 \mu_0 v^2 = \frac{v^2}{c^2}$$ Учитывая малость скорости $v \ll c$, то $$\boxed{\frac{F_B}{F_E} \approx 0}$$