$9.2.14^*.$ Прямой провод имеет виток радиуса $R$. По проводу течет ток $I$. Определите индукцию магнитного поля в центре витка и на его оси на расстоянии $h$ от его центра.
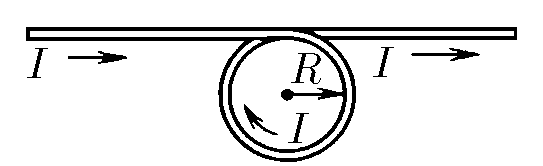
Разобьём систему на отдельно провод и кольцо с током с соответствующими им полями $B_1 $ и $B_2$
Из школьного курса известно, что поле бесконечного провода $$B_1 = \frac{\mu_0I}{2\pi l} = \frac{\mu_0 I}{2\sqrt{R^2 + h^2}}$$ Поле кольца мы находили в задаче 9.2.10: $$B_2 = \frac{\mu_0 I R^2}{2 (R^2 + h^2)^{3/2}}$$ Стоит отметить что $\vec{B_1}$ и $\vec{B_2}$ имеют разное направление, вектор $\vec{B_1}$ перпендикулярен плоскости точки и провода, а вектор $\vec{B_2}$ направлен вдоль оси. Несложно показать, что косинус угла между этими векторами $$\cos\gamma = \frac{R}{\sqrt{R^2+h^2}}$$ тогда
$$|\vec B| = |\vec B_1 + \vec B_2| = \sqrt{{B_1}^2+{B_2}^2+2B_1B_2\cos\gamma}$$
$$\boxed{B=\frac{\mu_0I}{2}\left[\frac{1}{\pi^2(R^2+h^2)} + \frac{R^4}{(R^2+h^2)^3} + \frac{2R^3}{\pi (R^2+h^2)^{5/2}}\right]^{1/2}}\quad(1)$$
При $h = 0$ подставляем в выражение $(1)$
$$B(0) = \frac{\mu_0I}{2R}\sqrt{\frac{1}{\pi^2} + 1 + \frac{2}{\pi}} \Rightarrow \boxed{B(0) = \frac{\mu_0I}{2\pi R}(1 + \pi)}$$
$$B(h)=\frac{\mu_0I}{2}\sqrt{\frac{1}{\pi^2(R^2+h^2)} + \frac{R^4}{(R^2+h^2)^3} + \frac{2R^3}{\pi (R^2+h^2)^{5/2}}}$$
$$B(0) = \frac{\mu_0I}{2\pi R}( \pi + 1)$$