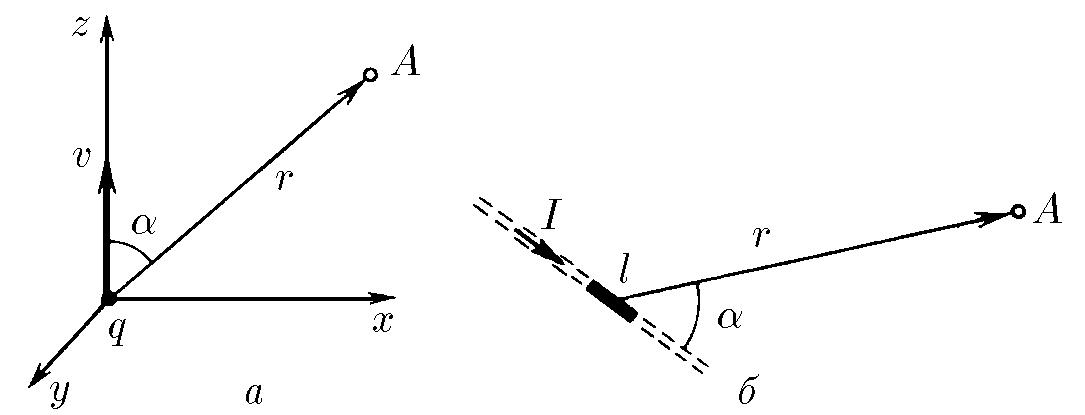
$9.2.8.$ а) Используя формулу, приведенную в задаче 9.2.1, определите индукцию магнитного поля, создаваемого зарядом $q$, движущимся со скоростью $v$, на расстоянии $r$ от этого заряда. Радиус-вектор $\vec{r}$ образует со скоростью $v$ угол $\alpha$.
б) Определите индукцию магнитного поля прямого провода длины $l$, по которому течет ток $I$, на расстоянии $r$ от провода, если $l \ll r$. Радиус-вектор $\vec{r}$ образует с проводом угол $\alpha$.
a) Запишем формулу, приведенную в задаче 9.2.1, $$\vec{B} = \mu_0 \varepsilon_0 [\vec{v} \times \vec{E}] \quad(1)$$ Cкорость течения тока найдём из 9.2.3 $$v = \frac{I}{\lambda}\quad(2)$$ Учитывая, что заряд $q = l\lambda$, напряженность электрического поля $$E = \frac{l\lambda}{4\pi\varepsilon_0r^2}\quad(3)$$ Подставляем $(2)$ и $(3)$ в $(1)$, и получаем выражаем $$ \vec{B} = \mu_0 \varepsilon_0\left[\vec{\left(\frac{I}{\lambda}\right)} \times \frac{l\lambda}{4\pi\varepsilon_0} \cdot \frac{\vec{r}}{r^3}\right] \quad(4)$$ $$\vec{B} = \frac{\mu_0 q}{4\pi r^3}[\vec{v} \times \vec{r}] $$ Модуль этого векторного произведения $$ B = \frac{\mu_0 q}{4\pi r^3}vr\cdot \sin\alpha \Rightarrow \boxed{B = \frac{\mu_0 qv}{4\pi r^2}\cdot \sin\alpha}$$
б) Так как $l \ll r$ то справедливо приближение нити как точечного заряда $$B = \mu_0 \varepsilon_0 Ev\cdot \sin\alpha$$ Подставляем выражения $v$ и $E$, из $(2)$ и $(3)$, соответственно $$B = \mu_0 \varepsilon_0 \frac{l\lambda}{4\pi\varepsilon r^2} \cdot \frac{I}{\lambda}\sin\alpha \Rightarrow \boxed{B=\frac{\mu_0Il}{4\pi r^2}\sin\alpha}$$
$$ B=\frac{\mu_0 qv}{4\pi r^2} \sin\alpha; \quad B = \frac{\mu_0 Il}{4\pi r^2}\sin\alpha$$